Преобразование Абеля. Признаки Дирихле и Абеля

Пусть — последовательность частичных сумм ряда — последовательность частичных сумм
ряда \(\sum_{n=1}^{\infty} b_n\). Возьмём m > n ≥ 1, тогда

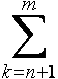a_kb_k = a_n+1b_n+1 + ... + a_mb_m = a_n+1(B_n+1 − B_n) + a_n+2 (B_n+2 − B_n+1) + ... + a_m (B_m − B_m−1) =

перегруппируем = − a_n+1B_n + (a_n+1 − a_n+2) B_n+1 + ... + (a_m−1 − a_m) B_m−1 + a_m B_m =

= − a_n+1 B_n + a_mB_m + (a_k − a_k+1) B_k.

Преобразование Абеля

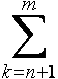a_kb_k = − a_n+1B_n + a_mB_m + 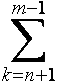(a_k − a_k+1) B_k.

Теорема

Признак Дирихле

Пусть

1.

2. — последовательность частичных сумм ограничена по совокупности, т. е. ∃ M > 0: ∀ n ⇒ |B_n| ≤ M,

тогда сходится.