Лемма Жордана и несобственные интегралы
Доказательство1
Будем понимать все рассматриваемые интегралы в смысле главного значения. Тогда, действуя аналогично решению примера 11.2, мы получим формулы (11.1) – (11.2).
Формулы (11.3) – (11.4) получатся из (11.1) – (11.2), если учесть, что произведение нечётной функции на sin αx (как и чётной функции на cos αx ) есть чётная функция, а для чётной функции 
(x) верно равенство:
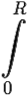
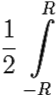
(x)dx = 
(x)dx
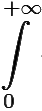cos αxf(x)dx = 
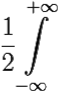cos αxf(x)dx в случае чётной f(x);
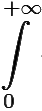sin αxf(x)dx =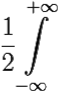sin αxf(x)dx в случае нечётной f(x).
Заметим, что в отличие от Леммы Жордана, нам пришлось потребовать в условии данного следствия, чтобы f(z) была аналитична не только в Im z > 0, но и на самой действительной оси (Im z ≥ 0). Это необходимо, чтобы мы могли применить основную теорему о вычетах к интегралу по контуру CR, содержащему отрезок [−R, R] действительной оси.
1 Формулы (11.1) – (11.4) надо понимать следующим образом: если интеграл, стоящий в левой части сходится, то непременно к числу, стоящему в правой части; а если расходится, то он сходится в смысле главного значения и его главное значение равно числу, стоящему в правой части. Заметим, что для сходимости всех этих интегралов достаточно, чтобы f(x) монотонно стремилась к нулю при x → ±∞.
