Преобразование Лапласа

Оценим |F(p)|:

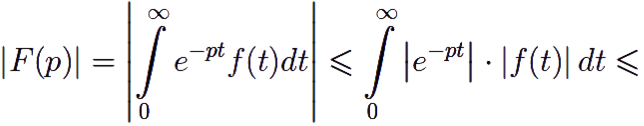
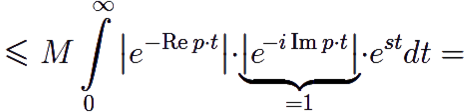
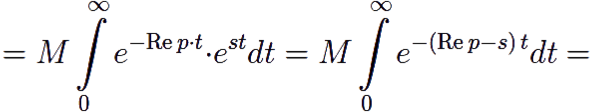
Таким образом, интеграл (12.1) сходится в произвольной точке p полуплоскости Re p > α.

Итак, для всех функций f(t) и Λ(α) определена функция:

F(p) = = e−ptf(t)dt,  Re p > α

(12.2)

Определение 12.3

Интеграл 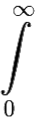e^−ptf(t)dt называется преобразованием Лапласа функции f(t).

При этом функция F(p), определённая по формуле (12.2) при p ∈ : Re p > α, называется изображением функции f(t), а функция f(t) называется оригиналом функции F(p). И то, и другое обозначается так:

F(p) f(t),   f(t) F(p).