Преобразование Лапласа
Утверждение 12.2
Условие
f(t) ∈ Λ(α).
Утверждение
При всех p ∈ ![]() , для которых Re p > α сходится интеграл
, для которых Re p > α сходится интеграл
F(p) = |
(12.1) |
Доказательство
Фиксируем произвольное p ∈ ![]() , для которого Re p > α. Тогда найдётся s такое, что,
, для которого Re p > α. Тогда найдётся s такое, что,
α < s < Re p.
В силу утверждения 12.1, для этого s ∃ M, при котором верно неравенство
|f(t)| ≤ Mest при всех t ≥ 0.


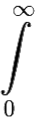 e−ptf(t)dt
e−ptf(t)dt
