Преобразование Лапласа

Здесь мы воспользовались тем, что для изменения порядка интегрирования достаточно равномерной по параметру сходимости всех участвующих в преобразованиях интегралов.

Кроме того, что отметить, что приведённое доказательство опирается на легко проверяемый факт, что степень роста свёртки функций равна максимальной из степеней роста сворачиваемых функций.

6) F⁽ⁿ⁾(p) = 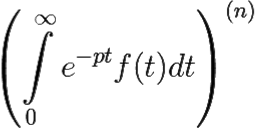= e^−pt−(t)ⁿf(t)dt (−1)ⁿtⁿf(t).

7) F(s)ds = e^−stf(t)dt ds =

= [в силу равномерной сходимости можно менять порядок интегрирования] =

= f(t)dte^−stds = f(t).

8) F(p + λ) = e^−(p+λ)tf(t)dt = e^−pt(e^−λtf(t))dt e^−λtf(t).