Несобственные интегралы

Интегралы вида f(x)dx

Для данного типа интегралов можно построить аппарат, весьма похожий на Лемму Жордана и способ её применения.

Лемма 11.2

Условие

1) f(z) аналитична в верхней полуплоскости Im z > 0, за исключением конечного числа изолированных особых точек .

2) zf(z) 0 при z → ∞, Im z > 0 равномерно относительно arg z.

Утверждение

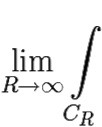f(z)dz = 0,

где C_R = {z: |z| = R, arg z ∈ (0, π)} — дуга окружности с центром в z = 0 и радиусом R в верхней полуплоскости.

Доказательство

Нам дано, что zf(z) 0 при z → ∞, Im z > 0 равномерно относительно arg z. Это означает, что при |z| = R с достаточно большим R имеет место оценка

|f(z)| < ,   |z| = R,   M(R) 0.

Поэтому

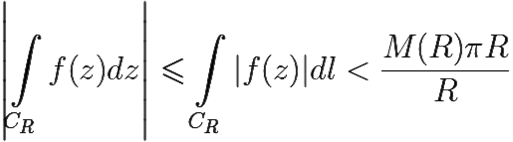= πM(R) → 0 при R → +∞.