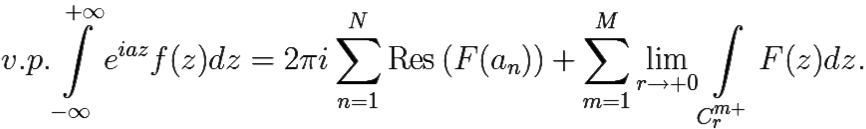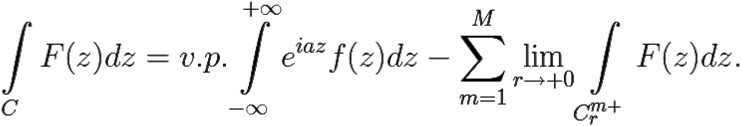Несобственные интегралы с полюсами на оси

Доказательство

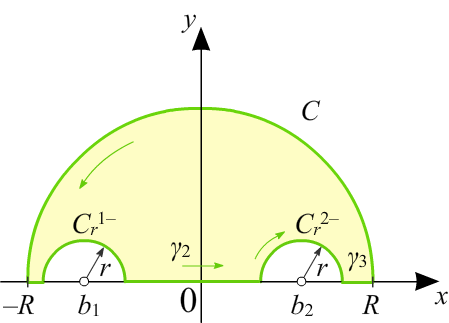
Рассмотрим контур C = , где — верхняя половинка окружности радиуса r с центром в b_m, проходимая по часовой стрелке, а γ_m — отрезок прямой , примыкающей к слева. Внутри контура C при достаточно больших R содержатся все изолированные особые точки a_n функции F(z), и по основной теореме о вычетах

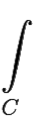F(z)dz = 2πi 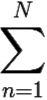Res (F(a_n)).

С другой стороны, при стремлении R → ∞, r → +0 в силу леммы Жордана получим, что левая часть данного равенства равна:

Отсюда,