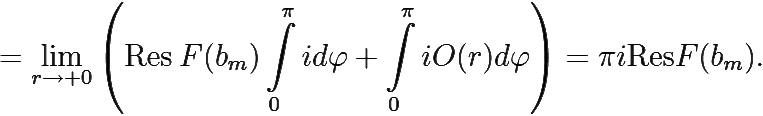Несобственные интегралы с полюсами на оси

Чтобы получить требуемую формулу, нам осталось вычислить

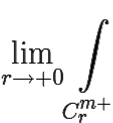F(z)dz.

Учтём, что b_m — полюс первого порядка, т. е. имеет место представление

F(z) = ,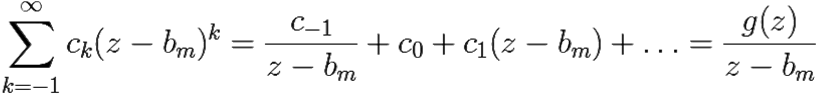

где (z) — аналитическая в окрестности b_m функция, причём

(b_m) = c₋₁ = Res F(b_m).

Отсюда, в силу аналитичности,

(z) = (b_m) + O(z − b_m) = Res F(b_m) + O(z − b_m), z → b_m

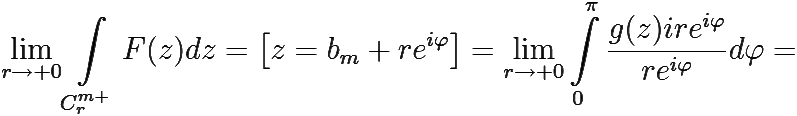
= [так как (z) = Res F(b_m) + O(r)] =