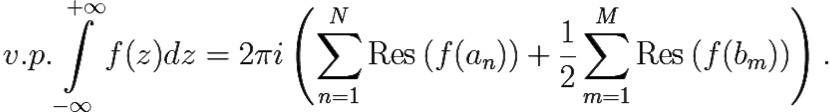Несобственные интегралы с полюсами на оси

Утверждение 11.2

Условие

1) f(z) аналитична в верхней полуплоскости Im z > 0, за исключением конечного числа изолированных особых точек .

2) f(z) имеет конечное число изолированных особых точек , b_m ∈ на прямой , все из которых являются полюсами первого порядка.

3) zf(z) 0 при z → ∞, Im z > 0 равномерно относительно arg z.

Утверждение

При a > 0