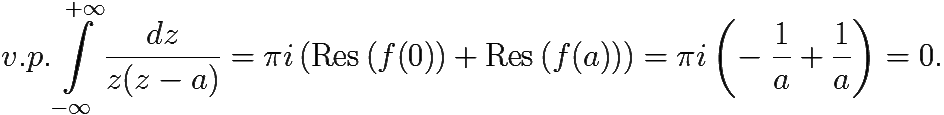Несобственные интегралы с полюсами на оси

Пример 11.4

Вычислить интеграл I = , a > 0.

Рассмотрим функцию комплексной переменной f(z) = . Она удовлетворяет требованиям утверждения 11.2:

1) f(z) аналитична в верхней полуплоскости Im z > 0, за исключением конечного числа изолированных особых точек . В данном случае особых точек в верхней полуплоскости вообще нет.

2) f(z) имеет конечное число изолированных особых точек , на прямой , все из которых являются полюсами первого порядка. В нашем случае — это точки b₁ = 0 и b₂ = a > 0.

3) zf(z) 0 при z → ∞, Im z > 0 равномерно относительно arg z.

Поэтому

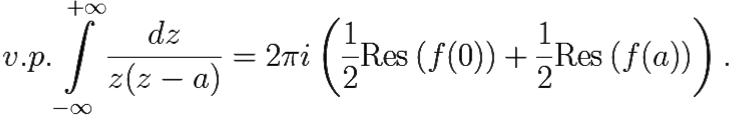
Найдём требуемые вычеты. По формуле (10.1) имеем:

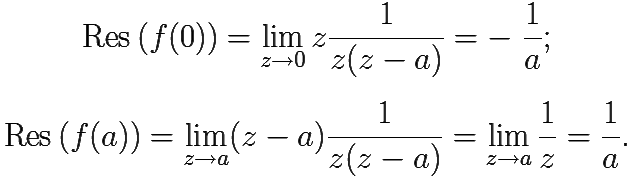
Итак,