Обращение преобразования Лапласа. Формула Меллина

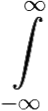e^−btf(t) = υ.p.e^−iytF(p)dy.

Надо отметить, что в последнем интеграле нельзя вынести F(p) из-под знака интеграла, так как p и y связаны соотношением
p = b − iy, и функция F(p) неявно зависит от переменной интегрирования.

Домножим обе части полученного равенства на e^bt и учтём, что мы ввели обозначение p = b − iy.

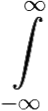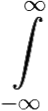f(t) = υ.p.e^bte^−iytF(p)dy ≡ υ.p.e^ptF(p)dy.

Вспомним, что p = b − iy ⇒ y = i(p − b), где b > α — фиксированное действительное число, и перепишем последнюю формулу:

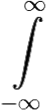f(t) = υ.p.e^ptF(p)dy = [y = i(p − b)] =

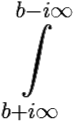= υ.p.e^ptF(p)dp =

= [меняем пределы интегрирования] = υ.p.e^ptF(p)dp.