Обращение преобразования Лапласа. Формула Меллина

Теорема 12.3

О представлении функции интегралом Фурье

Условие

φ(t) кусочно-непрерывно дифференцируема, и для неё сходится интеграл 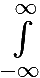φ(t)dt.

Утверждение

В каждой точке непрерывности φ(t) имеет место равенство

φ(t) =

(12.13)

В качестве функции φ(t) рассмотрим φ(t) = e^−btf(t) при некотором фиксированном b > α.

Тогда из формулы (12.13) получаем:

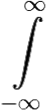e^−btf(t) = υ.p.e^−iyt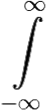e^iyxe^−bxf(x)dx dy =

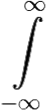= υ.p.e^−iyt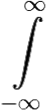e^{−(b − iy)x}f(x)dx dy = [p = b − iy] =

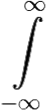= υ.p.e^−iyt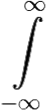e^−pxf(x)dx dy = υ.p.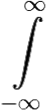e^−iytF(p)dy .