Обращение преобразования Лапласа. Формула Меллина
В рассмотренных примерах у нас получалось, что изображение искомого решения оказывалось табличной функцией, и его оригинал легко находился из таблицы. Разумеется, такими простыми случаями не ограничивается сфера применения преобразования Лапласа к решению интегральных и дифференциальных уравнений. Его сила в том, что оно сводит уравнение интегральное или дифференциальное к уравнению алгебраическому, из которого изображение искомого решения легко выражается. Однако получившегося выражения может не оказаться в таблице стандартных изображений. В таких случаях пользуются формулой обратного преобразования Лапласа — формулой Меллина (теорема 12.2).
Теорема 12.2
Формула Меллина
Условие
f(t) ∈ Λ(α) — кусочно-непрерывно дифференцируема, f(t) 
F(p).
Утверждение
f(t) =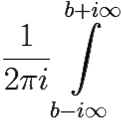 
eptF(p)dp, b > α,
где интеграл берётся по любой прямой, параллельной мнимой оси, лежащей в области Re z > α и понимается в смысле главного значения.
Доказательство
Нам понадобится теорема из курса математического анализа.
