Преобразование Лапласа

Определение 12.3

Интеграл 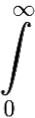e^−ptf(t)dt называется преобразованием Лапласа функции f(t).

При этом функция F(p), определённая по формуле (12.2) при p ∈ : Re p > α, называется изображением функции f(t), а функция f(t) называется оригиналом функции F(p). И то, и другое обозначается так:

F(p) f(t),   f(t) F(p).

Таблица преобразований Лапласа

1) 1 , Re p > 0;

2) t^ν , ν > −1, Re p > 0;

3) tⁿ , n ∈ , Re p > 0;

4) e^λt , Re p > Re λ;

5) sin at , Re p > |Im a|;

6) cos at , Re p > |Im a|;

7) sh at , Re p > |Re a|;

8) ch at , Re p > |Re a|.