Преобразование Лапласа
Доказательство
1) 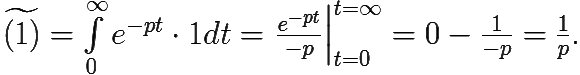
2) 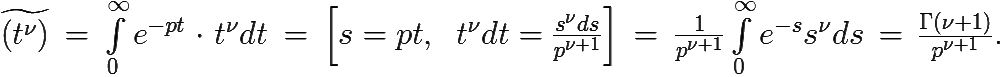
3) В силу свойства Гамма-функции: Г(n + 1) = n! для n = 0, 1, 2, … и предыдущего пункта.
4) 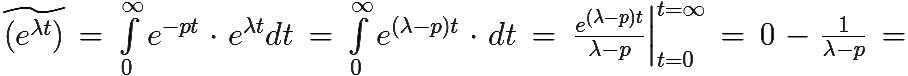
![]()
5) 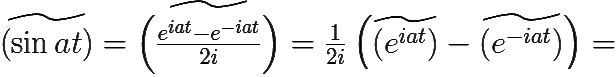
= [в силу пункта 4) при Re p > Re (±ia)] =
![]()
Re p > max {Re (ia), Re (−ia)} ≡ max {−Im a, Im a} ≡ |Im a|.

 Операционное исчисление и его приложения
Операционное исчисление и его приложения  Преобразование Лапласа
Преобразование ЛапласаДоказательство
1) 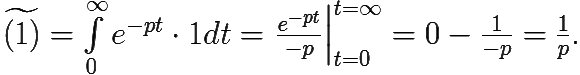
2) 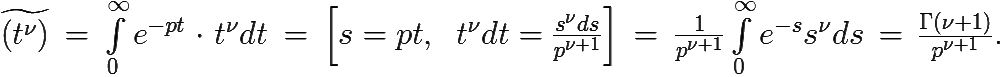
3) В силу свойства Гамма-функции: Г(n + 1) = n! для n = 0, 1, 2, … и предыдущего пункта.
4) 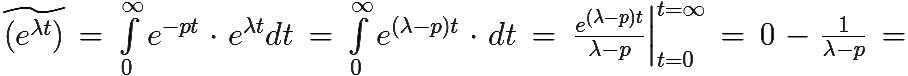
![]()
5) 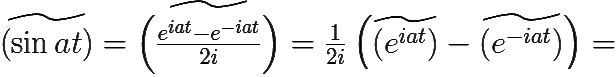
= [в силу пункта 4) при Re p > Re (±ia)] =
![]()
Re p > max {Re (ia), Re (−ia)} ≡ max {−Im a, Im a} ≡ |Im a|.