Критерий Коши равномерной сходимости ряда

⇐ (Достаточность)

1. Существование суммы ряда Φ(z). Функциональная последовательность S_n(z) = φ_k(z) в каждой точке z ∈ U является фундаментальной по условию теоремы и, следовательно, сходится к некоторому числу (сходимость фундаментальной последовательности на комплексной плоскости доказана в прошлой лекции). Обозначим это число через Φ(z) и получим функцию, являющуюся суммой данного ряда на множестве z ∈ U.

2. Равномерная сходимость ряда к функции Φ(z). Нам дано:

∀ ε > 0   ∃ N ∈ : ∀ n > N   ∀ p ∈    ∀ z ∈ U   .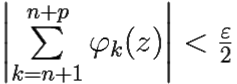

Поскольку неравенство 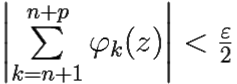выполнено при всех p ∈ , в нём можно перейти к пределу при p → ∞. Получим: