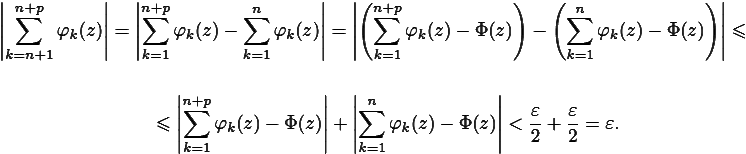Критерий Коши равномерной сходимости ряда

Теорема 3.3

Критерий Коши равномерной сходимости ряда

Утверждение

Функциональный ряд сходится равномерно на множестве U

   ⇔   ∀ ε > 0   ∃ N ∈ :

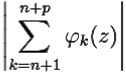∀ n > N   ∀ p ∈    ∀ z ∈ U     < ε.

Доказательство

⇒ (Необходимость)

Нам дано, что ряд сходится равномерно на U, то есть ∃ функция Φ(z):

∀ ε > 0   ∃ N ∈ : ∀ n ≥ N,   ∀ z ∈ U   .

Рассмотрим сумму