Признак Вейерштрасса

Теорема 3.4

Признак Вейерштрасса

Условие

|φ_k(z)| ≤ a_k при всех k ∈ и всех z ∈ D ⊆ . Числовой ряд a_k — сходится.

Утверждение

φ_k(z) сходится в D абсолютно и равномерно.

Доказательство

Так как числовой ряд a_k сходится, то по критерию Коши для числовых рядов (теорема 1.1)

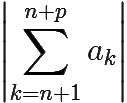∀ ε > 0   ∃ N(ε) ∈    ∀ n > N   ∀ p ∈ N    < ε.

Это означает, в силу неравенства 0 ≤ |φ_k(z)| ≤ a_k, что для того же N(ε)

∀ z ∈ U 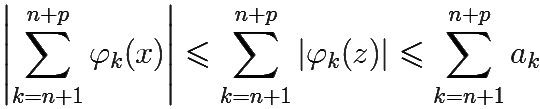   < ε,

откуда по критерию Коши ряд φ_n(x) сходится равномерно на U, то есть

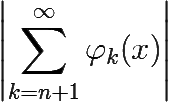∀ ε > 0   ∃ N(ε) ∈    ∀ n > N   ∀ z ∈ U    < ε.