Круговое свойство дробно-линейной функции

Функция ₂(z) = . Пусть действительная и мнимая части функции ₂(z) равны u(x, y) и υ(x, y). Тогда

Подставим в это уравнение окружности A(x² + y²) + Bx + Cy + D = 0, (|A| + |B| + |C| + |D| ≠ 0).

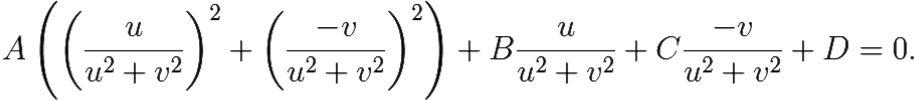
Отсюда, домножив на u² + υ², получим:

D(u² + υ²) + Bu − Cυ + A = 0, (|A| + |B| + |C| + |D| ≠ 0).

(Заметим, что окружности, проходящие через начало координат (D = 0), отобразятся в прямые (A = 0) — в окружности, проходящие через начало координат.)