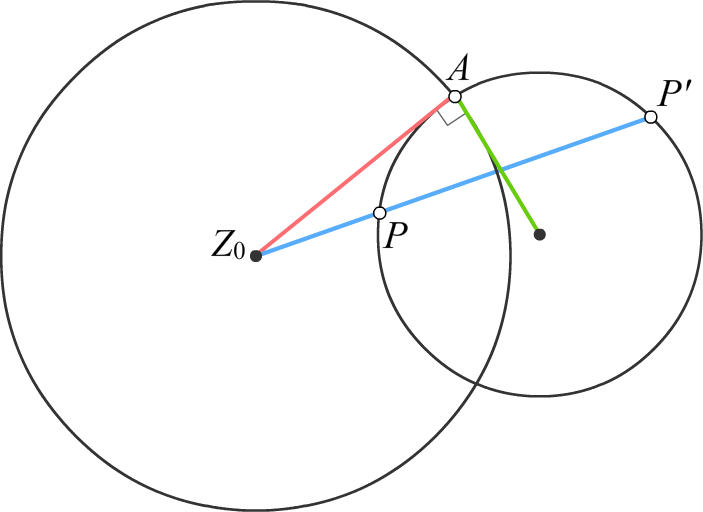
Леммы об окружностях
Лемма 5.1
Условие
Точки P и P′ симметричны относительно окружности |z − z0| = R.
Утверждение
Любая окружность, проходящая через точки P и P′, ортогональна к окружности |z − z0| = R (то есть пересекается с ней под прямым углом).
|
|
В самом деле, проведём любую окружность через точки P и P′, симметричные относительно окружности |z − z0| = R. Проведём из точки z0 касательную ко второй окружности и обозначим точку касания через A. По теореме 5.5, выполнено равенство |z0 − A|2 = |z0 − P| · |z0 − P′|. С другой стороны, по определению симметричных точек, |z0 − P| · |z0 − P′| = R2. Поэтому |z0 − A| = R, то есть точка A лежит и на окружности |z − z0| = R. |
В силу этого, радиусы, проведённые в точку касания, перпендикулярны друг другу, следовательно, окружности пересекаются под прямым углом.