Леммы об окружностях

Лемма 5.2

Условие

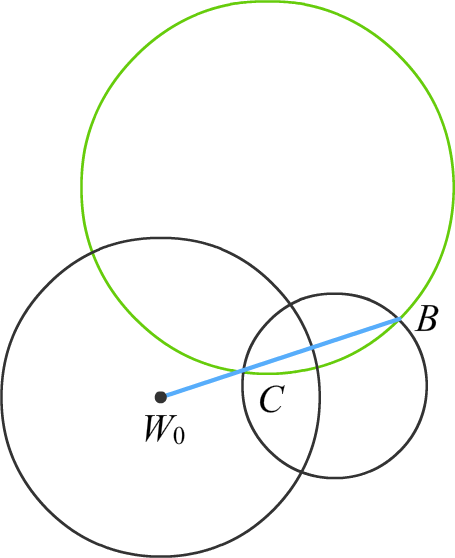
Пара окружностей, ортогональных окружности | − ₀| = , пересекаются в точках B и C.

Утверждение

Точки B и C симметричны относительно окружности | − ₀| = .

В самом деле, возьмём пару окружностей, ортогональных данной к окружности | − ₀| = . Обозначим их точки пресечения через B и C. Проведём прямую из центра ₀ окружности в точку C. Она является секущей к обеим ортогональным окружностям. Пусть она пересекает одну окружность в точке B*, а другую в точке B**. Тогда, по теореме 5.5 о касательной и секущей, верны равенства:

= |₀ − C| · |₀ − B*| = |₀ − C| · |₀ − B**|.

Но точки B* и B** лежат на одном луче, следовательно, эти равенства могут иметь место только в случае, когда эти точки совпадают:

B* = B**.

Таким образом, пара ортогональных окружностей пересекается в точках C и B = B* = B**, и эти точки симметричны относительно исходной окружности | − ₀| = .

Замечание 5.8

Обе леммы доказаны для окружностей, понимаемых обычным образом. Для случая окружностей бесконечного радиуса, то есть прямых, эти леммы также верны, и их доказательство в этом случае очевидно.

6/22