Интегральная теорема Коши

Доказательство

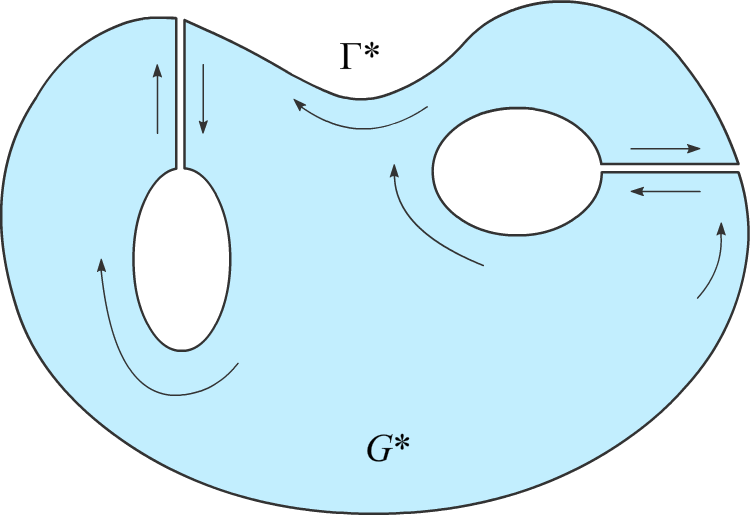
Соединим отдельные куски границы Г области G отрезками, лежащими в G, и назовём полученный контур, состоящий из кусков Г и добавленных отрезков, контуром Г*. Он является замкнутым и ограничивает односвязную область G*, совпадающую с областью G, разрезанную добавленными нами отрезками. При этом контур Г* целиком лежит в области аналитичности функции f(z), следовательно, по теореме Коши для односвязной области, f(z)dz = 0.

Но по свойству аддитивности интеграла, f(z)dz = f(z)dz + сумма интегралов по добавленным отрезкам, причём каждый отрезок проходится сначала в одном направлении,, затем в противоположном. Поэтому сумма интегралов по добавленным отрезкам равна нулю, и мы получаем, что f(z)dz = 0.