Первообразная

Определение 6.2

Аналитическая функция F(z) называется первообразной аналитической функции f(z) в области D, если всюду в D выполнено равенство F′(z) = f(z).

Определение 6.3

Неопределённым интегралом от аналитической функции f(z) в области D называется множество всех её первообразных.

Теорема 6.4

Условие

f(z) непрерывна в области D. Интеграл от f(z) по любому замкнутому контуру, лежащему в D, равен 0.

Утверждение

Функция F(z) = 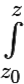f(ζ)dζ является

1) аналитической в D,

2) первообразной для f(z) в D.