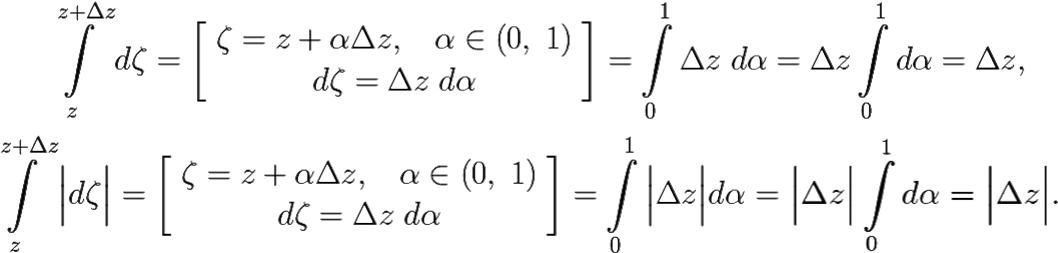Первообразная

Доказательство

Шаг 1

Составим разностное отношение:

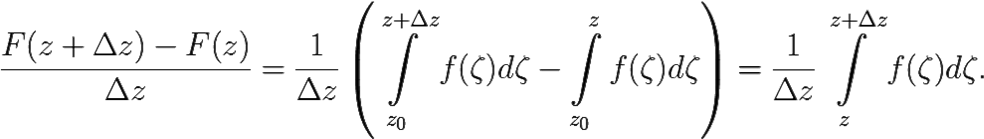
Последнее равенство имеет место в силу независимости значения интеграла 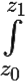f(ζ)dζ от пути интегрирования и второго свойства из теоремы 6.1.

Шаг 2

Выберем в качестве пути интегрирования в последнем интеграле отрезок, соединяющий точки z и z + Δz. Это удобно, поскольку в этом случае легко проверить соотношения 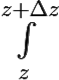dζ = Δz и 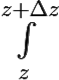|dζ| = |Δz|.

Действительно, параметризуем отрезок от z до z + Δz: ζ = z + αΔz, α ∈ (0, 1), тогда