Первообразная

Шаг 3

Оценим разность:

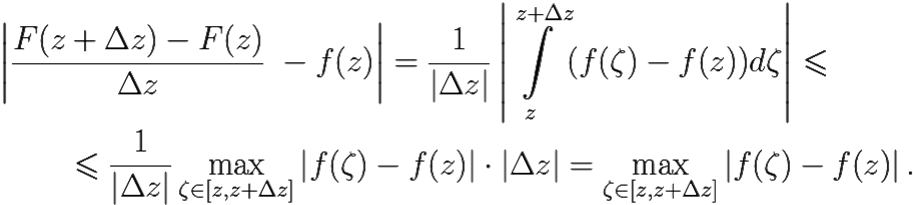
В силу непрерывности f(z) в точке z, f(ζ) = f(z), откуда |f(ζ) − f(z)| = 0.

Таким образом, существует

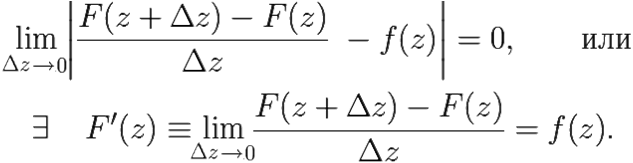
Убедившись в наличии у F(z) производной в произвольной точке z ∈ D, мы автоматически доказали аналитичность F(z) в D.