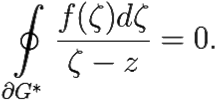Интегральная формула Коши
Теорема 6.5
Интегральная формула Коши
Условие
f(z) аналитична в области D. Область G 
D имеет границу δG = C.
Утверждение
Для произвольной точки z ∈ G имеет место равенство
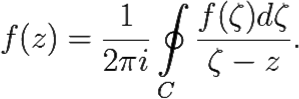
Доказательство
|
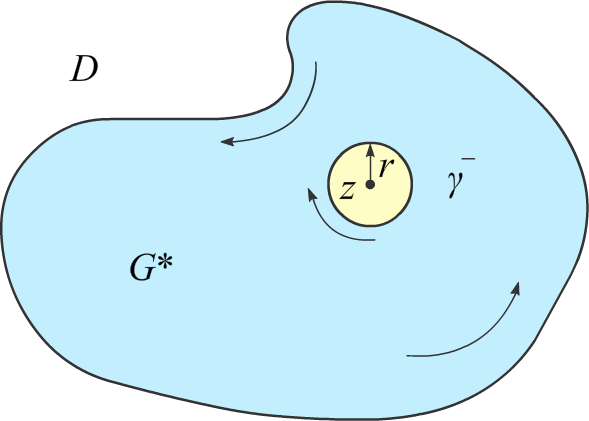
Выбросим из области G кружок радиуса r с центром в точке z. Если область G была n-связной, то полученная после выкидывания круга область G* будет (n + 1)-связной. При этом в области G* подынтегральная функция аналитична т. к. числитель и знаменатель аналитичны в G*, и знаменатель ζ − z не обращается в ноль в G*. Поэтому, по теореме Коши для многосвязной области
|
17/20
