Интегральная формула Коши

Устремив r → +0, получим, что два последних слагаемых стремятся к нулю, а первое, не зависящее от r, есть некоторое число:

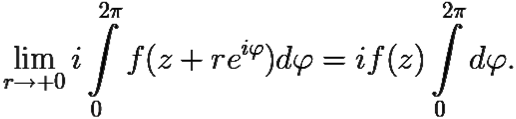
Возьмём интеграл в правой части: и окончательно получим:

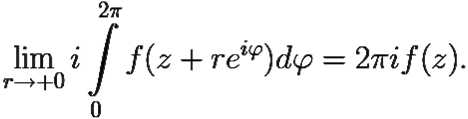
Из (6.5) и последней формулы получаем:

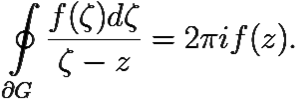
Замечание 6.1

Доказанная теорема даёт ещё одно неожиданное свойство аналитических функций: достаточно знать значения аналитической функции на некотором замкнутом контуре, чтобы по ним найти её значения во всех точках внутри этого контура. Это в очередной раз подчёркивает, насколько сильным является условие аналитичности: если функция задана на границе некоторой области, мы не можем её продолжить внутрь области так, как захотим, поскольку её значения внутри области уже определены однозначно. В то же время непрерывные, и даже n раз непрерывно дифференцируемые функции двух действительных переменных можно продолжать и внутрь области бесконечным числом различных способов с сохранением их гладкости.