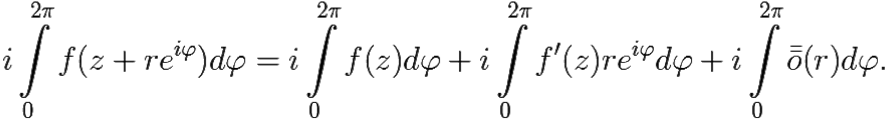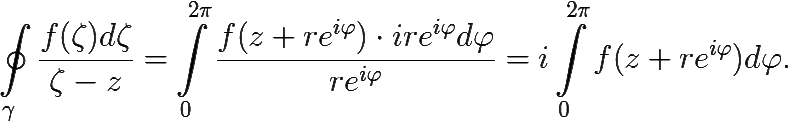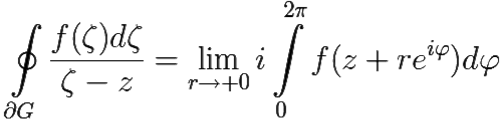Интегральная формула Коши

Тогда

(6.4)

Принципиально важным моментом здесь является то, что мы вывели формулу (6.3) для произвольного радиуса r (достаточно малого, чтобы контур γ не пересекался с границей области G). Поэтому можно перейти в (6.3) к пределу при r → +0 . При этом левая часть (6.3) не зависит от r, следовательно, не изменится.

(6.5)

В правой части, в силу дифференцируемости функции f(z) имеем:

f(z + re^iφ) = f(z) + f ′(z)[(z + re^iφ) − z] + [(z + re^iφ) − z] = f(z) + f ′(z)re^iφ + (r),   r → 0.

Таким образом, интеграл правой части (6.5) ведёт себя следующим образом: