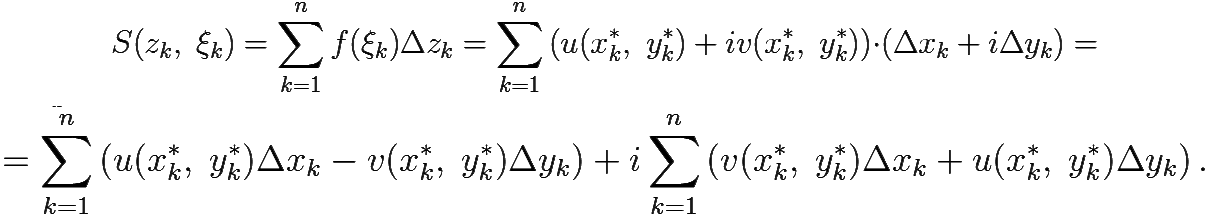Интеграл функции комплексного переменного
Понятие и свойства интеграла функции комплексного переменного
Определение 6.1
Интегралом от функции f(z) вдоль кривой C называется число, равное:
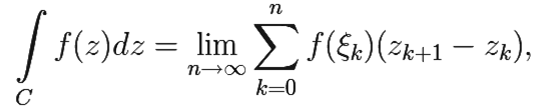
где z0 = a, z1, z2, ..., zn+1 = b последовательные точки, разбивающие C на n участков, через a и b обозначены концы C, ξk произвольная точка, лежащая на участке от zk до zk+1 кривой C, а предел берётся в предположении, что |zk+1 − zk| → 0.
Пусть z = x + iy, ξk = xk* + iyk*, Δz = Δx + iΔy, а f(z) = u(x, y) + iυ(x, y).
Тогда интегральная сумма S(zk, ξk) = ![]() f(ξk)Δzk интеграла
f(ξk)Δzk интеграла ![]() f(z)dz запишется в виде:
f(z)dz запишется в виде: