Интеграл функции комплексного переменного

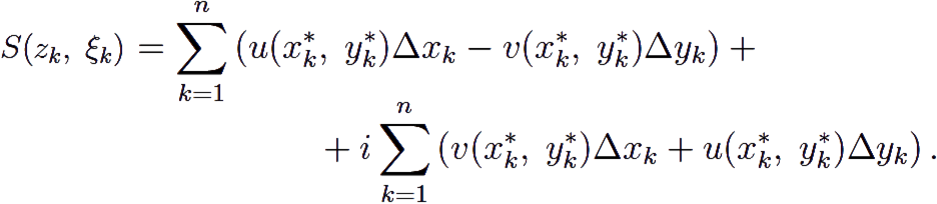
Но суммы, стоящие в правой части этого равенства, представляют собой интегральные суммы криволинейных интегралов

u(x, y)dx − υ(x, y)dy и υ(x, y)dx + u(x, y)dy.

Поэтому, если существуют данные криволинейные интегралы, то существует и интеграл f(z)dz, причём выполнено равенство:

f(z)dz = udx − υdy + iυdx + udy.

(6.1)

Эта формула позволяет свести вычисление интеграла от функции комплексного переменного к криволинейному интегралу II-го рода функций двух действительных переменных.

Из курса анализа известно, что если C — кусочно-гладкая кривая, а f(z) (и, следовательно, функции u и υ) — кусочно-непрерывная ограниченная функция, то интегралы

u(x, y)dx − υ(x, y)dy и υ(x, y)dx + u(x, y)dy

(и, следовательно, интеграл f(z)dz) существуют.