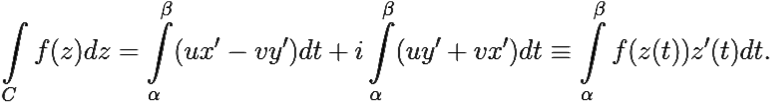Интеграл функции комплексного переменного

Для вычисления этих интегралов на практике удобно пользоваться обычным приёмом для вычисления криволинейных интегралов — параметризацией контура и сведением криволинейного интеграла к обычному интегралу Римана.

Рассмотрим

f(z)dz = (u + iυ) d (x + iy) = udx − υdy + iυdx + udy.

Если x = x(t), y = y(t) — параметризация контура С, причём (x(α), y(α)) — начало, а (x(β), y(β)) — конец кривой С, то

(6.2)

Действительно, f(z(t))z′(t) = (u + iυ)(x′ + iy′) = (ux′ − υy′) + i(υx′ + uy′).

Поскольку имеет место такая связь интеграла от функции комплексного переменного с криволинейным интегралом II-го рода функций двух действительных переменных, то все свойства интегралов распространяются и на случай интеграла от функции комплексного переменного.