Интеграл функции комплексного переменного

Теорема 6.1

Свойства интеграла

Условие

f(z) и (z) интегрируемы вдоль контура С = С₁ + С₂ (то есть C является объединением С₁ и С₂, не имеющих общих внутренних точек).

Утверждение

∀ c₁, c₂ ∈

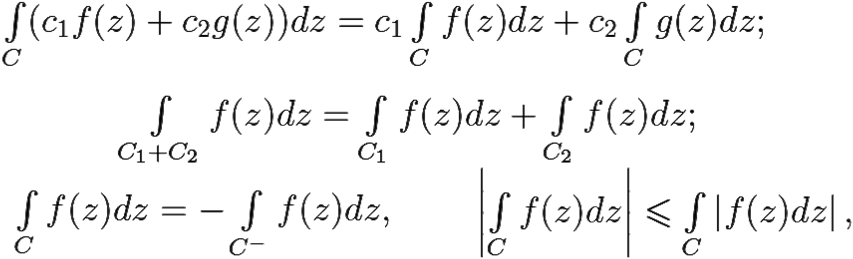
где С⁻ — кривая, совпадающая с С, но проходимая в противоположном направлении.