Интегральная теорема Коши

Доказательство

Сведём вычисление интеграла от функции комплексного переменного к криволинейному интегралу II-го рода функций двух действительных переменных:

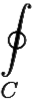f(z)dz = 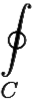udx − υdy + i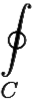υdx + udy.

Из курса III-го семестра известна формула Грина: пусть контур C есть граница области G, а функции P(x, y) и Q(x, y) непрерывно дифференцируемы в G, тогда:

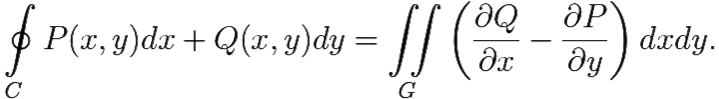
Применим к нашим интегралам эту формулу:

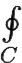udx − υdy = 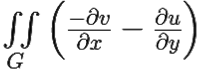dxdy = [в силу условий Коши–Римана] = 0dxdy = 0.

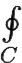υdx + udy = 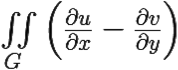dxdy = [в силу условий Коши–Римана] = 0dxdy = 0.

Таким образом, 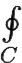f(z)dz = 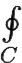udx − υdy + i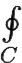υdx + udy = 0 + i · 0 = 0.