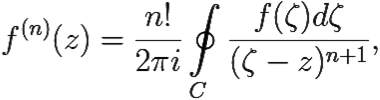Бесконечная дифференцируемость аналитической функции

Утверждение 6.1

Аналитичность интеграла, зависящего от параметра.

Условие

φ(z, ζ) аналитична по z в односвязной области D и ограничена в D × C (то есть при z ∈ D и ζ ∈ C).
При этом φ, ∈ C(D × C). Взаимное расположение D и C совершенно произвольно.

Утверждение

Функция F(z) = φ(z, ζ)dζ аналитична в D, и

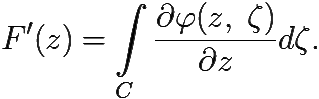
Теорема 6.6

Производные всех порядков у аналитической функции.

Условие

f(z) аналитична в области D. Область G D имеет границу ∂G = C.

Утверждение

При любом n ∈ функция f⁽ⁿ⁾(z) аналитична в G. Для произвольной точки z ∈ G имеет место равенство

n = 0, 1, 2, ....

(6.6)