Бесконечная дифференцируемость аналитической функции

Доказательство

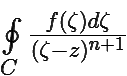Фиксируем производную точку z₀ ∈ G. Рассмотрим область G₀, такую, чтобы ⊂ G₀ и z₀ ∈ G₀. Тогда интеграл является собственным при всех z ∈ G₀, а его подынтегральная функция φ(z, ζ) =  аналитична по z в G₀, ограничена и непрерывна вместе с по совокупности примерных в G₀ × C. Поэтому мы можем применить утверждение 6.1. Оно гарантирует нам, что функция, стоящая в правой части (6.6) аналитична в G₀ и, в частности, в точке z₀, и её производную можно найти формальным дифференцированием под знаком интеграла. Поскольку точку z₀ ∈ G мы выбирали произвольно, то вывод об аналитичности правой части (6.6) и о дифференцировании её под знаком интеграла можно распространить на всю область G.

При n = 0 формула (6.6) совпадает с интегральной формулой Коши (теорема 6.5), значит она не требует проверки. При произвольном n > 0 формула (6.6) получается формальным дифференцированием интегральной формулы Коши n раз. Например, раз f(z) = 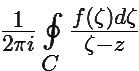, то

f ′(z) =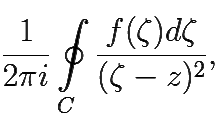

f ″(z) =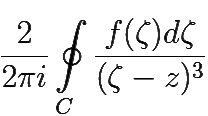

и так далее.