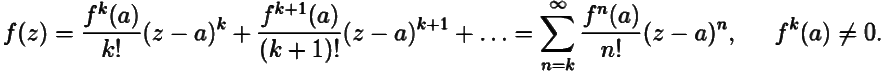Изолированные нули

Доказательство

Поскольку f(z) 0 ни в какой окрестности точки a, то её ряд Тейлора обязан содержать отличные от нуля члены. Пусть номер первого члена, отличного от нуля, есть k.

(7.2)

Тогда a нуль порядка k функции f(z). Поделим равенство (7.2) на (z − a)^k. Получим:

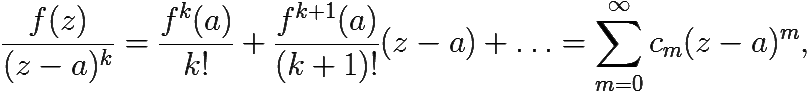
где . Ряд в правой части является степенным, следовательно, сходится в круге некоторого радиуса R. На самом деле, R равняется радиусу сходимости ряда (7.2), поскольку, по формуле Коши–Адамара он вычисляется как предел корней степени n из модулей коэффициентов ряда (7.2). Обозначим функцию, к которой он сходится, через φ(z).

φ(z) = c_m(z − a)^m

Заметим, что φ(a) = ≠ 0. При этом по теореме 7.8 ряд c_m(z − a)^m является рядом Тейлора функции φ(z), причём φ(z) аналитична внутри круга сходимости. Из аналитичности

φ(z) = u(x, y) + iυ(x, y)

cледует непрерывность функции u(x, y) и υ(x, y) в точке a. Хотя бы одна из функций u(x, y) и υ(x, y) не равна нулю в a, т. к. φ(a) ≠ 0, и по теореме о сохранении знака непрерывной функцией она не обратится в нуль в некоторой окрестности точки a. Отсюда f(z) = φ(z)(z − a)^k также не обратится в нуль в той же окрестности нигде, кроме точки z = a.