Теорема единственности

1) Если D ⊆ G, то теорема доказана.

2) Предположим, что D\G = M ≠ ∅.

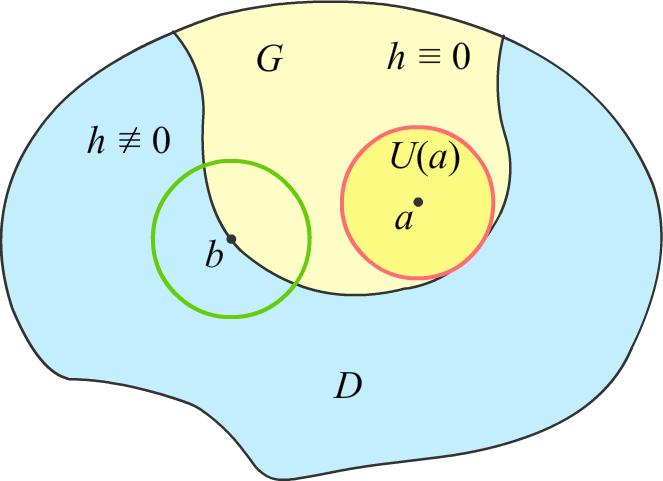
Тогда, по крайней мере часть границы ∂G лежит в D. Рассмотрим любую точку b этой части границы ∂G.

С одной стороны, раз она на границе G, то в любой её окрестности есть точки, в которых h(z) = 0.

C другой стороны, раз она на границе G, то h(z) 0 в любой окрестности точки b. Следовательно, по теореме 7.9 об изолированных нулях, h(z) не имеет других нулей, кроме b в некоторой окрестности b.

Полученное противоречие говорит о том, что наше предположение, что D\G = M ≠ ∅ является неверным. Таким образом, h(z) ≡ 0 всюду в D.

Но h(z) = f(z) − (z) ⇒ f(z) ≡ (z), z ∈ D.