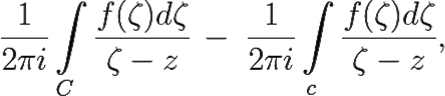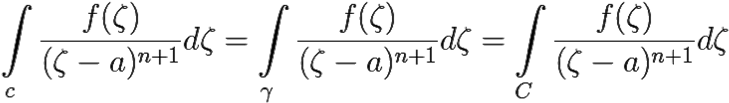Ряд Лорана
Рассмотрим кольцо
K = {z: r′ < |z − a| < R′},
где r < r′ < R′ < R, целиком лежащее в K. Заметим, что мы выбрали K′ так, чтобы и фиксированная в начале доказательства точка z, и окружность γ попали внутрь K′.
Обозначим окружности, ограничивающие кольцо K′, через
с = {z: |z − a| = r′} и C = {z: |z − a| = R′}.
Поскольку функция f(z) аналитична в K′ и на её граничных контурах c и C, то мы имеем право воспользоваться интегральной формулой Коши (теорема 6.5). Итак, ∀ z ∈ K′
f(z) = |
(8.4) |
где обе окружности c и C проходятся против часовой стрелки.
Далее, так как для произвольной окружности γ радиуса ρ: r′ < ρ < R′ с центром в точке z = a функция f(z) аналитична в области, содержащей c, γ и C, то следующие три интеграла равны:
|
(8.5) |
(В самом деле, чтобы убедиться, что равны, например, два последних интеграла в (8.4), надо рассмотреть область, ограниченную контурами γ и C, применить в ней интегральную теорему Коши).
Теперь рассмотрим ряд из (8.1) в произвольной фиксированной точке z ∈ K′.