Неравенства Коши

Следствие 8.1

Условие

f(z) аналитична в круге B = {z: |z − a| < R}, и ограничена |f(z)| ≤ M на окружности γ = {z: |z − a| = ρ}, где 0 < ρ < R.

Утверждение

Для функции f и её производных f⁽ⁿ⁾ в точке z = a выполнены неравенства Коши:

(8.10)

Доказательство

Пользуясь тем, что ряд Тейлора аналитической в круге {z: |z − a| < R} функции f(z) является её же рядом Лорана в кольце {z: 0 < |z − a| < R}, по теореме 8.3 получаем, что для коэффициентов с_n, n ∈ {0, 1, 2, …} выполнены неравенства Коши (8.9).

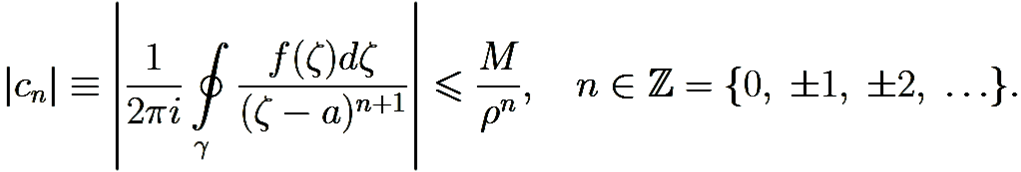
Умножим их на n! при n ≥ 0, учтём формулы (6.6)

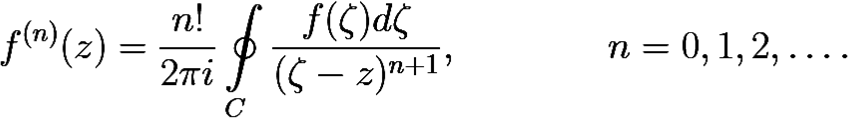
и получим равенство (8.10).