Ряд Тейлора

Второй переход можно делать, если ряд сходится равномерно в области, содержащей C. Заметим, что сходимость ряда должна быть равномерна относительно переменной, по которой происходит интегрирование, т. е. по ζ. Но при произвольном фиксированном z ∈ {|z − a| < r}

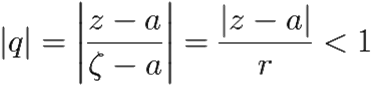
z ∈ {|z − a| < r} — фиксированное число

откуда по признаку Вейерштрасса равномерной сходимости функциональных рядов ряд сходится равномерно по ζ в любой области, где |q| ≤ const < 1, в частности, на контуре C.

Третий переход возможен при таких z и ζ, для которых |q| < 1, то есть для z ∈ {|z − a| < r}, ζ ∈ C это действие правомочно.

Итак, равенство (7.1) доказано для всех z ∈ {|z − a| < r}. Но поскольку для любой z ∈ {|z − a| < R} можно так подобрать число r < R, чтобы точка z оказалась внутри z ∈ {|z − a| < r}, то равенство (7.1) верно всюду в круге сходимости z ∈ {|z − a| < R}.

Равномерная сходимость в любой замкнутой подобласти данного ряда, в силу того, что он степенной, следует из утверждения 3.2.