Ряд Тейлора

Доказательство

Пусть функция f(z) аналитична в круге {|z − a| < R}.

Рассмотрим окружность

C = {ζ: |ζ − a| = r} при некотором r < R.

Фиксируем произвольную точку z ∈ {|z − a| < r} и выпишем цепочку равенств:

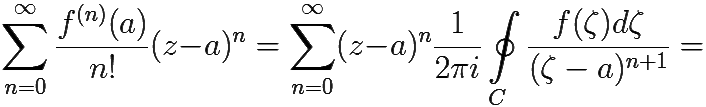
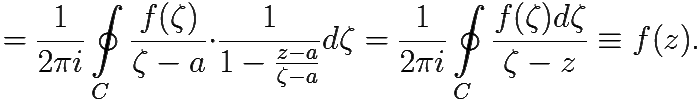
При этих выкладках мы воспользовались: при первом переходе теоремой о производных всех порядков аналитической функции, при втором — теоремой 7.1 о почленном интегрировании равномерно сходящегося ряда, при третьем — формулой суммы геометрической прогрессии, при последнем — интегральной формулой Коши (теорема 6.5). Осталось выяснить, при каких же z проведённые преобразования правомочны.

Первый и последний переходы имеет право на существование при всех z, принадлежащих области аналитичности f(z) внутри контура C, то есть в круге {|z − a| < r}.