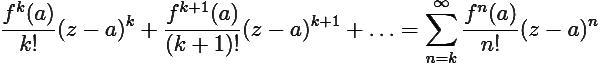Изолированные нули

Определение 7.1

1) Точку z = a мы будем называть нулём аналитической функции f(z), если f(a) = 0.

2) Точку z = a мы будем называть нулём порядка k аналитической функции f(z), если

f(a) = f ′(a) = … = f^k − 1(a) = 0 и f^k(a) ≠ 0.

Если разложить аналитическую функцию f(z), имеющую в точке a нуль порядка k, в ряд Тейлора с центром в точке a, то, очевидно, первые его k слагаемых равны нулю:

f(z) = .

(7.2)

Теорема 7.9

Об изолированных нулях

Условие

f(z) аналитична в окрестности своего нуля z = a и не равна тождественно нулю ни в какой его окрестности.

Утверждение

Существует окрестность точки z = a, в которой f(z) не имеет других нулей. (Другими словами z = a — изолированный нуль функции f(z).)