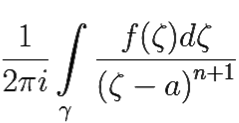Ряд Лорана

Разложение аналитической в кольце функции в ряд

Мы выяснили, что функцию, аналитическую в круге, можно и притом единственным образом разложить в степенной ряд — ряд Тейлора, который будет сходиться к данной функции внутри круга аналитичности. А что делать, если заданная функция аналитична в области иного вида, например, всюду в круге {z: |z − a| < R} кроме самой точки z = a, то есть в кольцевой области
{z: 0 < |z − a| < R}? Оказывается, что для функций, аналитических в кольцевых областях {z: r < |z − a| < R}, где
0 ≤ r < R ≤ ∞, можно простроить разложения по положительным и отрицательным степеням (z − a). Данное разложение является обобщением изученного нами ряда Тейлора.

Теорема 8.1

Лоран, 1843 г.

Условие

f(z) аналитична в кольце K = {z: r < |z − a| < R}, где 0 ≤ r < R ≤ ∞.

Утверждение

В кольце K справедливо равенство

f(z) = cn(z − a)n.

(8.1)

с коэффициентами

cn = ,

(8.2)

где γ = {z: |z − a| = ρ} — окружность произвольного радиуса ρ ∈ (r, R), лежащая в K, причём в любой замкнутой подобласти K ряд Лорана (8.1) сходится к f(z) равномерно.