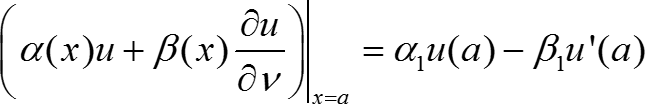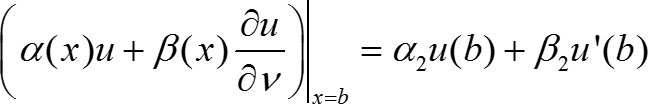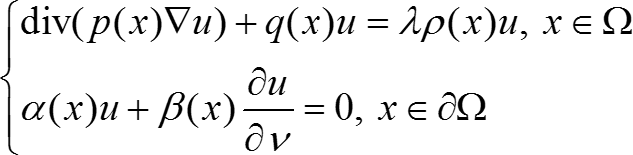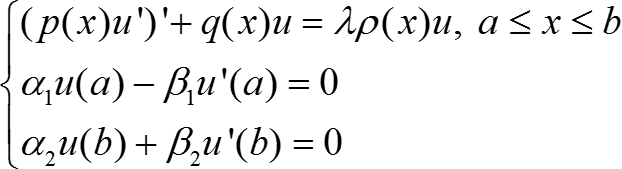Многомерная задача Штурма–Лиувилля. Свойства оператора. Свойства собственных функций и собственных значений

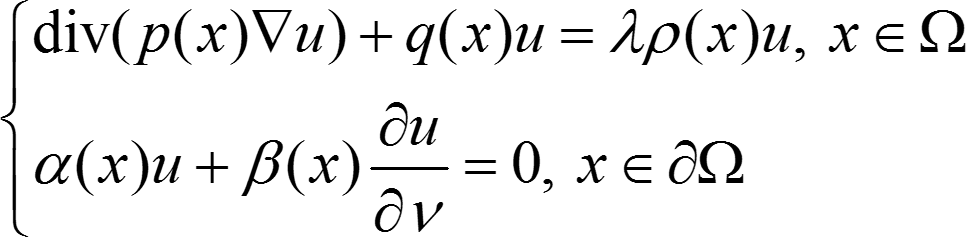
Задача

Найти все значения параметра λ (собственное значение), при которых система имеет нетривиальное (не равное тождественно нулю) решение (собственная функция).

Пример

(n = 1)  Ω = (a; b), Ω = {a; b}, = [a; b]

νa = {−1}, νb = {1} α(a) = α1, β(a) = β1, α(b) = α2, β(b) = β2	div(p(x)∇u) = (p(x)u′)′