Решение второй задачи. Принцип Дюамеля

ν(x, t) = tM[φ] = 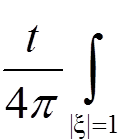φ(x + atξ)dS_ξ

u(x, t) = ν_t(x, t)

ν(x, t) ∈ C³(x ∈ R³, t ≥ 0) ⇒ u(x, t) ∈ C²(x ∈ R³, t ≥ 0)

ν_tt = a²Δν ⇒ (ν_tt)_t = a²(Δν)_t ⇒ (ν_t)_tt a²Δ(ν_t)_t ⇒ u_tt = a²Δu

ν(x, 0) = 0, ν_t(x, 0) = φ(x) ⇒ u(x, 0) = φ(x)

ν_tt(x, t) = 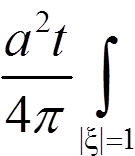Δφ(x + atξ)dS_ξ ⇒ u_t(x, 0) = ν_tt(x, 0) = 0