Разбиение задачи на три. Решение первой задачи. Метод средних значений
u(x, t) = 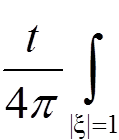 ψ(x + atξ)dSξ
ψ(x + atξ)dSξ
Δu(x, t) = 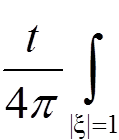 Δψ(x + atξ)dSξ
Δψ(x + atξ)dSξ
ut(x, t) = 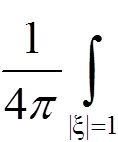 ψ(x + atξ)dSξ +
ψ(x + atξ)dSξ + 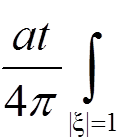 (∇ψ, ξ)dSξ
(∇ψ, ξ)dSξ
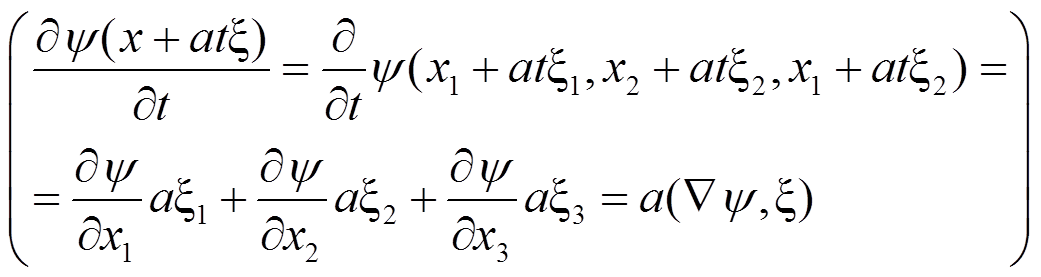
I = 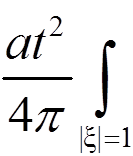 (∇ψ, ξ)dSξ ⇒ ut =
(∇ψ, ξ)dSξ ⇒ ut = ![]()

 Формула Кирхгофа
Формула Кирхгофа  Разбиение задачи на три. Решение первой задачи. Метод средних значений
Разбиение задачи на три. Решение первой задачи. Метод средних значений u(x, t) = 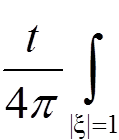 ψ(x + atξ)dSξ
ψ(x + atξ)dSξ
Δu(x, t) = 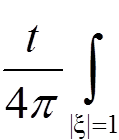 Δψ(x + atξ)dSξ
Δψ(x + atξ)dSξ
ut(x, t) = 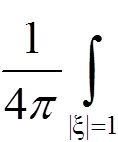 ψ(x + atξ)dSξ +
ψ(x + atξ)dSξ + 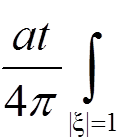 (∇ψ, ξ)dSξ
(∇ψ, ξ)dSξ
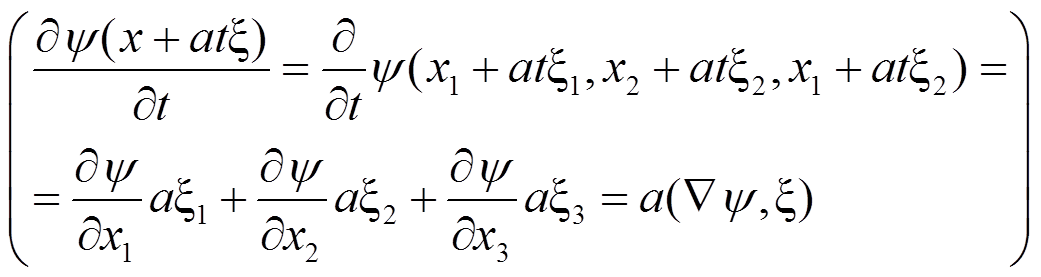
I = 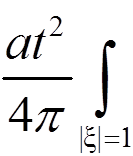 (∇ψ, ξ)dSξ ⇒ ut =
(∇ψ, ξ)dSξ ⇒ ut = ![]()