Теорема Лиувилля

Теорема Лиувилля

Если гармоническая во всём пространстве функция ограничена сверху или снизу, то она постоянна.

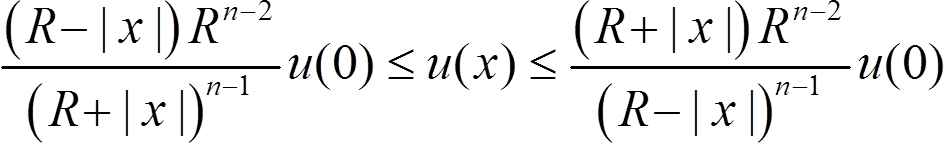
R → ∞

u(0) ≤ u(x) ≤ u(0) ⇒ u(x) ≡ u(0)

2) u(x) ≥ m ⇒ v(x) = u(x) − m ≥ 0 ⇒ v(x) ограничена ⇒ u(x) ограничена

3) u(x) ≤ M ⇒ v(x) = −u(x) ≥ −M ⇒ v(x) ограничена ⇒ u(x) ограничена