Пьезоэлектрические преобразователи

Пьезопреобразователи — электромеханические преобразователи, принцип действия которых основан на пьезоэлектрическом эффекте — явлении возникновения электрической поляризации под действием механических напряжений. Если пьезоэлектрическую пластинку с нанесёнными электродами (пьезоэлемент) подвергнуть действию механических напряжений (сжатию, растяжению, сдвигу), то на её поверхности появятся электрические заряды за счёт поляризации (прямой пьезоэффект или эффект Кюри). Приложение электрического напряжения к электродам вызывает механическую деформацию пьезоэлемента (обратный пьезоэффект, эффект Джоуля).

Для изготовления пьезопреобразователей используют следующие классы анизотропных материалов

анизотропные кристаллы естественного происхождения: кварц, турмалин;
синтетические кристаллы: сегнетова соль, ниобат лития;
поляризованные поликристаллические сегнетоэлектрики, получаемые методами керамического производства (пьезокерамика): титанат бария $\mathrm{BaTiO_{3}}$, цирконат-титанат свинца $\mathrm{PbZrO_{3}} - \mathrm{PbTiO_{3}}$ — пьезокерамика ЦТС.

Появились пьезополимерные (обычно плёночные) преобразователи, которые могут быть нанесены на поверхность любого профиля. Наиболее перспективные из них — полимерные плёнки ПВДФ.

Пьезоэлектрические свойства преобразователей характеризуют константами, связывающими механические величины: напряжение $T$ и деформацию $S$ с электрическими: напряжённостью электрического поля $E$ и электрической индукцией $D$. Система уравнений, описывающих работу пьезопреобразователя, должна включать: уравнение движения упругой среды; уравнения, связывающие механические напряжения и деформации; уравнения для прямого и обратного пьезоэффектов.

Так как все пьезоэлектрики существенно анизотропны, их свойства зависят от направления относительно кристаллических осей или осей поляризации, поэтому для описания свойств пьезоэлектрических материалов используют тензорные представления теории электроупругости. Так, компонента тензора механических напряжений $T_{ik}$ есть $i$-я компонента ($i=1,2,3$ ) силы $F$, действующей на единицу поверхности площадью $f$, перпендикулярной оси $x_{k}$, в соответствии с соотношением: $F_{i}=T_{ik}f_{k}$. Например, на единичную площадку, перпендикулярную оси $x$ (ось $1$), в общем случае могут действовать нормальное напряжение $T_{11}$ и касательные (сдвиговые) напряжения $T_{21}$ и $T_{31}$.

Точно так же компоненты тензора деформаций с совпадающими индексами соответствуют деформациям растяжения — сжатия, а с различающимися индексами — сдвиговым деформациям. Таким образом, тензор деформаций, как и тензор напряжений, характеризуется девятью компонентами, представимыми в форме матрицы:

(10.1)

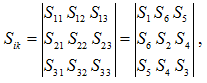
Вторая запись матрицы, учитывающая равенство компонент $S_{21}=S_{12},S_{31}=S_{13},S_{23}=S_{32}$, более удобна, в ней компоненты $S_{1},S_{2},S_{3}$ соответствуют линейным деформациям растяжения — сжатия, а компоненты $S_{4},S_{5},S_{6}$ — сдвиговым деформациям. Такая же запись используется и для тензора напряжений, записываемого в виде условного $6$-мерного вектора $T_{ik}={T_{1},T_{2},T_{3},T_{4},T_{5},T_{6}}$, где первые три компоненты соответствуют нормальным напряжениям, а три вторые — сдвиговым. При такой упрощённой форме представления закон Гука запишется в виде:

$$T_{i}=\sum_{k=1}^6 c_{ik}S_{k}$$

(10.2)

где коэффициенты $c_{ik}$ — константы упругости, общее число которых сокращается до $36$. Так как реальные кристаллы обладают симметрией и, кроме того, многие коэффициенты равны нулю, количество констант упругости много меньше максимально возможного их числа. Так, у кварца отличны от нуля 6 компонент, у пьезокерамики ЦТС — $5$ компонент.

Диэлектрические свойства кристаллов выражаются тензором диэлектрической проницаемости $ε_{ik}$, связывающим между собой компоненты векторов индукции и напряжённости электрического поля в пьезоэлектрике:

$$D_{i}=\sum_{k-1}^3 ε_{ik}E_{k}$$

или в упрощённой записи

$D_{i}=ε_{ik}E_{k},$ где $(k = 1,2,3).$

(10.3)

Отметим, что значения компонент тензора $ε_{ik}$ зависят от условий механического нагружения пьезоэлемента, а именно, находится он при постоянной по объёму механической деформации или подвержен постоянному механическому напряжению, в соответствии с чем различают компоненты $ε_{ik}^{S}$ и $ε_{ik}^{T}$. Так же и величина константы упругости пьезоэлемента зависит от того, каков электрический режим работы преобразователя, и различается для случаев постоянной электрической индукции $D$ и постоянной напряжённости электрического поля $E$, что отражается соответствующим индексом при обозначении константы: $c_{ik}^{D}$ и $c_{ik}^{E}$.

2/3