Эквивалентные схемы пьезопреобразователей

Эквивалентная схема пьезопреобразователя, описывающая продольные или толщинные колебания пьезодатчика в виде стержня или пластины и справедливая в широком интервале частот, может быть представлена в виде шестиполюсника (так называемая схема Редвуда):

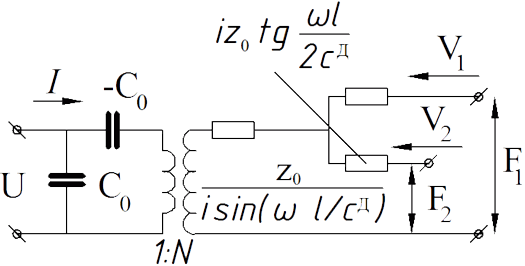
Эта схема соответствует наличию у преобразователя двух механических и одной электрической пары зажимов. В режиме излучения $U$ — электрическое напряжение, приложенное к электродам, а в режиме приёма — выходное электрическое напряжение преобразователя. $F_1$ и $F_2$ — силы, действующие на концах стержня или пластины. Электромеханический трансформатор с размерным коэффициентом трансформации $N$ (вольт/ньютон) формально отражает взаимовлияние механических и электрических параметров преобразователя. Если преобразователь нагружен только с одной стороны, то сила на другой стороне равна нулю и это отражается замыканием одной пары механических зажимов. Возбуждающая сила оказывается приложенной ко второй паре и компенсируется инерционной силой колебаний преобразователя.

Значения параметров схемы для пластины из пьезокерамики ЦТС, колеблющейся по толщине, равны:

$$C_0=\frac{\varepsilon^{S}_{33}S_0}{l}; Z_0=\rho c^D S_0;c^D=\sqrt{c^{D}_{33}/\rho};N=\frac{e_{33}S_{0}}{l},$$

(11.4)

где $C_0$ — собственная ёмкость пластины толщиной l и площадью $S_0$; $Z_0$ — характеристический импеданс датчика; $\rho$ — плотность материала датчика; $c^D$ — скорость продольной волны, определяемая константой упругости $c_{33}^D$ и плотностью материала $\rho$; N — коэффициент трансформации; $e_{33}$ — пьезоэлектрическая константа.

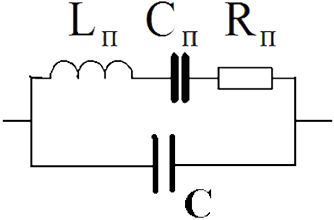
На частотах, близких к резонансным, эквивалентная схема пьезопреобразователя может быть приведена к виду:

В этой схеме электрический импеданс преобразователя $Z_{эл}$ представлен в виде собственной ёмкости $C_0$ пьезопластины и сопротивления диэлектрических потерь $R_{эп}$, влиянием которого обычно можно пренебречь. Параметр $R_n$характеризует потери энергии на излучение в окружающую среду и трение (сопротивление потерь), а параметры $L_n,C_n$ отражают влияние массы преобразователя и его упругой податливости (гибкости) на характер колебаний.

Приведённая схема может быть использована для определения основных пьезоэлектрических и механических характеристик преобразователя. Вблизи одной из резонансных частот ненагруженный пьезоэлектрический преобразователь можно представить в виде двухполюсника, полученного из эквивалентной схемы шестиполюсника, замыканием накоротко обеих пар механических клемм (т. е. полагая $F_1=0$ и $F_2=0$):

Используя эту схему, можно измерить собственную электрическую ёмкость датчика $C_0$ и частоты последовательного и параллельного резонансов цепи:

$$\omega_{посл}=\frac{1}{\sqrt{L_nC_n}},\omega_{пар}=\left[\frac{1}{L_nC_n}\left(1+\frac{C_n}{C_{0}}\right)\right]^{1/2}$$

(11.5)

Частоты последовательного и параллельного резонансов, соответствующие максимуму и минимуму полной проводимости цепи, позволяют оценить значения резонансной $f_p$ и антирезонансной $f_a$ частот датчика как механической системы. Используя эти значения, а также измеряя минимальные и максимальные значения импеданса датчика, можно рассчитать пьезоэлектрические константы и коэффициент электромеханической связи. Подробно последовательность измерений и расчётов изучаются студентами в соответствующей лабораторной работе.

3/4