Ёмкостные преобразователи

Ёмкостный преобразователь представляет собой конденсатор, электрические параметры которого изменяются под действием входной величины. Конденсатор состоит из двух электродов, к которым подсоединены выводные концы. Пространство между электродами может быть заполнено диэлектриком. При изменении взаимного положения электродов или при изменении диэлектрической проницаемости среды, заполняющей межэлектродное пространство, изменяется ёмкость конденсатора.

В качестве ёмкостного преобразователя часто используют плоский конденсатор. Его ёмкость определяется выражением:

$$C_{0}=\frac{ε ε_{0}S_{0}}{\delta },$$

(12.1)

где $\delta$ — расстояние между электродами; $S_{0}$ — их площадь; $ε_{0}$ — диэлектрическая постоянная; $ε$ — относительная проницаемость диэлектрика.

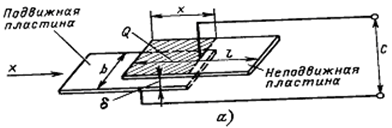
Изменение любого из трёх параметров ($\delta,S_{0},ε$) изменяет ёмкость конденсатора. У преобразователя с прямоугольными электродами площадью $S_{0}=bx$ имеется некоторый диапазон перемещения пластин $х$, в котором ёмкость линейно зависит от х: $C=εε_{0}bx/\delta$. Искажением линейной зависимости вследствие краевого эффекта пренебрежём.

В области линейной зависимости чувствительность такого преобразователя постоянна и увеличивается с уменьшением расстояния между электродами $\delta$:

$$S=dC/dx=εε_{0}b/\delta.$$

(12.2)

Обычно этот тип датчика реализуется в виде поворотного конденсатора для измерения угловых смещений, а не в виде варианта со сдвигом, приведённого на рисунке.

Если изменяется расстояние $\delta$ между электродами, функция преобразования $C=f(\delta)$ — не линейна и представляет собой гиперболическую характеристику. Чувствительность такого преобразователя:

$$S=|dC/d\delta|=εε_{0}S_{0}/\delta ^{2}=C_{0}/\delta$$

(12.3)

сильнее, чем в предыдущем случае, зависит от расстояния между пластинами $\delta$. Для увеличения чувствительности целесообразно уменьшение $\delta$, т. к. чувствительность возрастает как $1/\delta ^{2}$. Предельное значение $\delta$ определяется технологическими параметрами и приложенным напряжением. Следует учесть, что при большой напряжённости поля возможен электрический пробой воздушного промежутка.

Если перемещать диэлектрическую пластину в зазоре плоского конденсатора (см. рисунок $а$), то можно получить преобразователь с переменной диэлектрической проницаемостью.

Ёмкость такого преобразователя определяется как ёмкость двух параллельно включённых конденсаторов. Один из них $C_{ε}$ образован частью электродов и диэлектрической пластиной, другой $C_{1}$ — оставшейся частью электродов с межэлектродным пространством, не заполненным пластинкой. Если пластинка с относительной диэлектрической проницаемостью $ε$ имеет толщину $\delta$, равную расстоянию между электродами, то функция преобразования преобразователя описывается выражением:

$$C_{0}=C_{1}+C_{ε}=\frac{ε_{0}S_{1}}{\delta}+\frac{εε_{0}S_{ε}}{\delta}=\frac{ε_{0}}{\delta}(S_{1}+εS_{ε})=\frac{ε_{0}}{\delta}[S_{0}+(ε-1)S_{ε}]$$

(12.4)

где $S_{0}$ — площадь электродов; $S_{ε}$ — часть площади диэлектрической пластины, находящаяся между электродами; $S_{1}=S_{0}-S_{ε};S_{ε}=bx$.

Чувствительность такого датчика постоянна и равна:

$$S=\frac{dC}{dX}=\frac{\partial C}{\partial S_{ε}}\cdot \frac{\partial S_{ε}}{\partial x}=(ε-1)\cdot b \cdot \frac{ε_{0}}{\delta}$$

(12.5)

Датчик с диэлектриком может быть реализован в другой модификации. Например, в форме двух концентрических цилиндров, и использован для измерения уровня жидкости в резервуаре. Непроводящая жидкость играет роль диэлектрика.

Ёмкостные преобразователи могут выполняться по дифференциальной схеме. Схема дифференциального преобразователя углового перемещения $\alpha$ с переменной площадью электродов приведена на рисунке б). В таких преобразователях средний подвижный электрод обычно соединяется с экранной обмоткой кабеля.

2/3